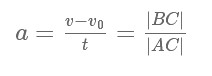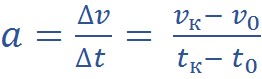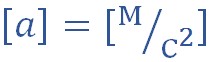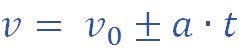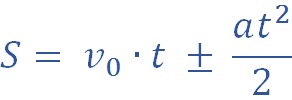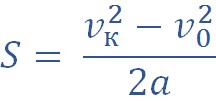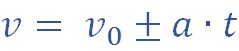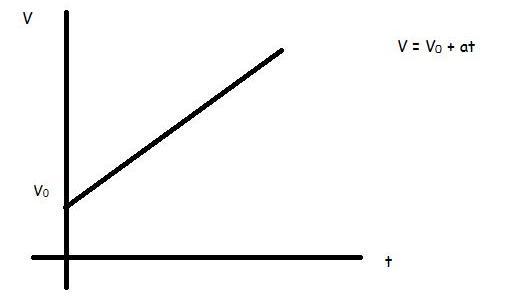в чем измеряется равноускоренное движение

Прямолинейное равноускоренное движение. Формулы и решение задач

Одним из самых распространенных видов перемещения объектов в пространстве, с которым человек встречается повседневно, является равноускоренное прямолинейное движение. В 9 классе общеобразовательных школ в курсе физики изучают подробно этот вид движения. Рассмотрим его в статье.

Кинематические характеристики движения

Прежде чем приводить формулы, описывающие равноускоренное прямолинейное движение в физике, рассмотрим величины, которые его характеризуют.

Вам будет интересно: Методика ШТУР: расшифровка аббревиатуры, особенности проведения теста, итоговый анализ и результаты

Вам будет интересно: «Рубаха-парень»: значение в прошлом и сейчас

Путь S и скорость v являются переменными характеристиками при прямолинейном равноускоренном движении. Ускорение же является величиной постоянной.

Связь скорости и ускорения

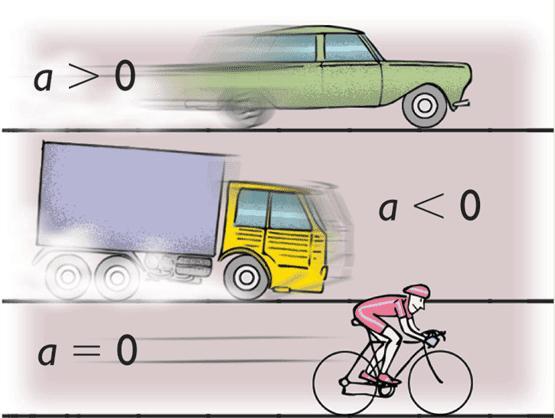
Представим себе, что некоторый автомобиль движется по прямой дороге, не меняя свою скорость v0. Это движение называется равномерным. В какой-то момент времени водитель стал давить на педаль газа, и автомобиль начал увеличивать свою скорость, приобретя ускорение a. Если начинать отсчет времени с момента, когда автомобиль приобрел ненулевое ускорение, тогда уравнение зависимости скорости от времени примет вид:

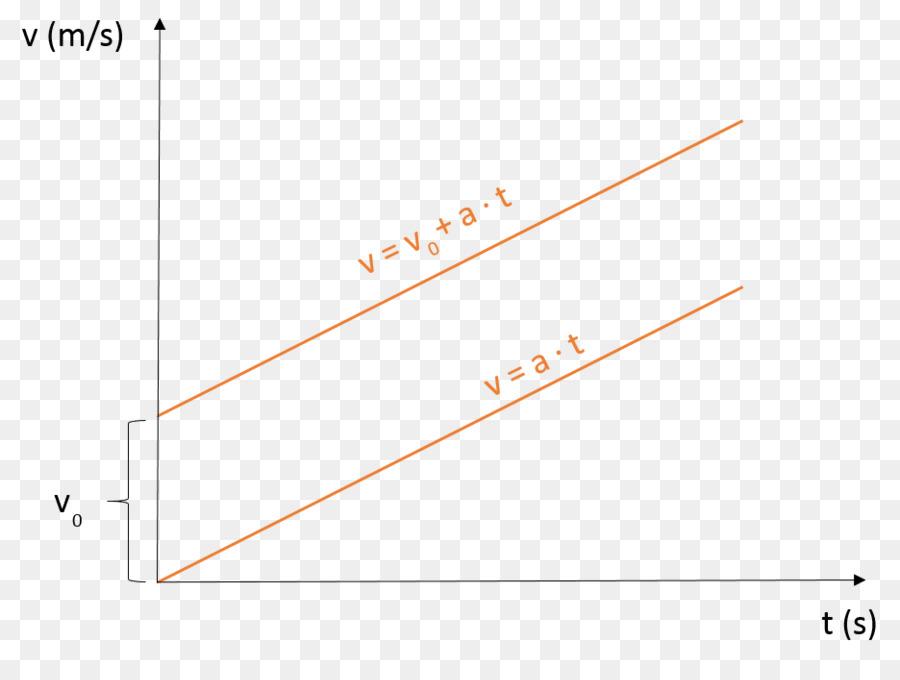
На рисунке показаны два графика. Отличие между ними заключается только в том, что верхний график соответствует скорости при наличии некоторого начального значения v0, а нижний описывает скорость равноускоренного прямолинейного движения, когда тело начало из состояния покоя ускоряться (например, стартующий автомобиль).

Отметим, если в примере выше водитель вместо педали газа нажал бы педаль тормоза, то движение торможения описывалось бы следующей формулой:

Этот вид движения называется прямолинейным равнозамедленным.

Формулы пройденного пути

На практике часто важно знать не только ускорение, но и значение пути, который за данный период времени проходит тело. В случае прямолинейного равноускоренного движения эта формула имеет следующий общий вид:

S = v0 * t + a * t2 / 2.

В случае торможения движущегося объекта выражение для пути примет вид:

В отличие от предыдущего случая здесь ускорение направлено против скорости движения, что приводит к обращению в ноль последней через некоторое время после начала торможения.

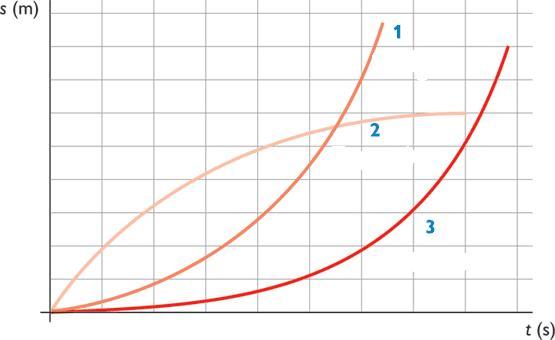
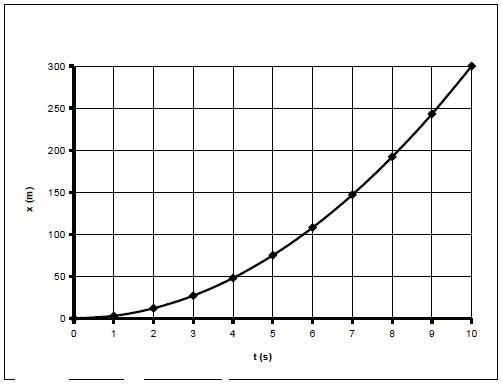
Не сложно догадаться, что графиками функций S(t) будут ветви параболы. На рисунке ниже представлены эти графики в схематическом виде.

Параболы 1 и 3 соответствуют ускоренному перемещению тела, парабола 2 описывает процесс торможения. Видно, что пройденный путь для 1 и 3 постоянно увеличивается, в то время как для 2 он выходит на некоторую постоянную величину. Последнее означает, что тело прекратило свое движение.

Далее в статье решим три разные задачи на использование приведенных формул.

Задача на определение времени движения

Автомобиль должен отвести пассажира из пункта A в пункт B. Расстояние между ними 30 км. Известно, что авто в течение 20 секунд движется с ускорением 1 м/с2. Затем его скорость не меняется. За какое время авто доставит пассажира в пункт B?

Расстояние, которое авто за 20 секунд пройдет, будет равно:

При этом скорость, которую он наберет за 20 секунд, равна:

Тогда искомое время движения t можно вычислить по следующей формуле:

Переведем все известные данные в систему СИ и подставим в записанное выражение. Получим ответ: t = 1510 секунд или приблизительно 25 минут.

Задача на расчет пути торможения

Теперь решим задачу на равнозамедленное движение. Предположим, что грузовой автомобиль двигался со скоростью 70 км/ч. Впереди водитель увидел красный сигнал светофора и начал останавливаться. Чему равен тормозной путь авто, если он остановился за 15 секунд.

Тормозной путь S можно рассчитать по следующей формуле:

Время торможения t и начальную скорость v0 мы знаем. Ускорение a можно найти из выражения для скорости, учитывая, что ее конечное значение равно нулю. Имеем:

Подставляя полученное выражение в уравнение, приходим к конечной формуле для пути S:

Подставляем значения из условия и записываем ответ: S = 145,8 метра.

Задача на определение скорости при свободном падении

Пожалуй, самым распространенным в природе прямолинейным равноускоренным движением является свободное падение тел в поле гравитации планет. Решим следующую задачу: тело с высоты 30 метров отпустили. Какую скорость будет оно иметь в момент падения на поверхность земли?

Искомую скорость можно рассчитать по формуле:

Время падения тела определим из соответствующего выражения для пути S:

Подставляем время t в формулу для v, получаем:

v = g * √(2 * S / g) = √(2 * S * g).

Значение пройденного телом пути S известно из условия, подставляем его в равенство, получаем: v = 24,26 м/с или около 87 км/ч.

Источник

Равноускоренное движение: формулы и примеры

Содержание:

Определение

Равноускоренным движением в физике считается такое движение, вектор ускорения которого не меняется по модулю и направлению. Говоря простым языком, равноускоренное движение представляет собой неравномерное движение (то есть идущее с разной скоростью), ускорение которого является постоянным на протяжении определенного промежутка времени. Представим себе автомобиль, который начинает двигаться, первые 2 секунды его скорость равна 10 м/с, следующие 2 секунды он уже движется со скоростью 20 м/с, а еще через 2 секунды уже со скоростью 30 м/с. То есть каждые 2 секунды он ускоряется на 10 м/с, такое движение и есть равноускоренным.

Отсюда можно вывести предельно простое определение равноускоренного движения: это такое движение любого физического тела, при котором его скорость за равные промежутки времени изменяется одинаково.

Примеры

Наглядным примером равноускоренного движения в повседневной жизни может быть велосипед, едущий с горки вниз (но не велосипед, управляемый велосипедистом), или брошенный камень под определенным углом к горизонту.

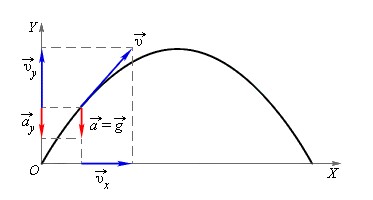
К слову пример с камнем можно рассмотреть более детально. В любой точке траектории полета на камень действует ускорение свободного падения g. Ускорение g не меняется, то есть остается константой и всегда направлено в одну сторону (по сути, это главное условие равноускоренного движения).

Полет брошенного камня удобно представить в виде сумы движений относительно вертикальной и горизонтальной оси системы координат.

Если вдоль оси Х движение камня будет равномерным и прямолинейным, то вдоль оси Y равноускоренным и прямолинейным.

Формула

Формула скорости при равноускоренном движении будет иметь такой вид:

Где V₀ – это начальная скорость тела, а – ускорение (как мы помним, эта величина является константой), t – общее время полета камня.

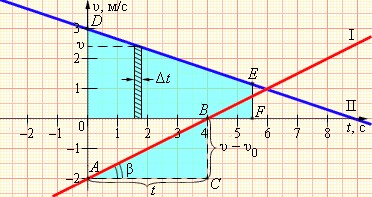
При равноускоренном движении зависимость V(t) будет иметь вид прямой линии.

Ускорение может быть определено по углу наклона графика скорости. На этом рисунке оно равно отношению сторон треугольника АВС.

Чем больше угол β, тем больше наклон и как следствие, крутизна графика по отношению к оси времени, и тем больше будет ускорение тела.

Рекомендуемая литература по теме

Видео

Автор: Павел Чайка, главный редактор журнала Познавайка

При написании статьи старался сделать ее максимально интересной, полезной и качественной. Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту pavelchaika1983@gmail.com или в Фейсбук, с уважением автор.

Похожие посты:

Один комментарий

Источник

Равноускоренное движение

Всего получено оценок: 123.

Всего получено оценок: 123.

Одним из видов движения, изучаемых кинематикой, является равноускоренное движение. Равноускоренное движение — это достаточно распространённый вид движения, даже большинство равномерных движений начинались с разгона и были некоторое время равноускоренными. Рассмотрим эту тему подробнее, получим формулу равноускоренного движения, приведём примеры такого движения.

Ускорение

Если некоторое тело начинает движение из состояния покоя, то его скорость изменяется от нуля до некоторого максимального значения. Следовательно, при таком движении можно указать быстроту изменения скорости.

Например, в рекламе автомобилей указывается время разгона до 100 км/ч. Ясно, что модель, достигающая такой скорости за 5 секунд, значительно резвее, чем модель со временем разгона 15 секунд, хотя конечная скорость в обоих случаях одинакова. В чем же здесь разница, с точки зрения кинематики?

Из данной формулы можно получить размерность ускорения. Скорость измеряется в метрах в секунду, а время — в секундах, значит, ускорение измеряется в метрах в секунду за секунду (или метров в секунду в квадрате).

В приведённом примере первый автомобиль разгоняется с ускорением 5,56 метров в секунду за секунду, а второй — с ускорением 1,85 метров в секунду за секунду.

Рис. 1. Ускорение в физике.

Равноускоренное движение

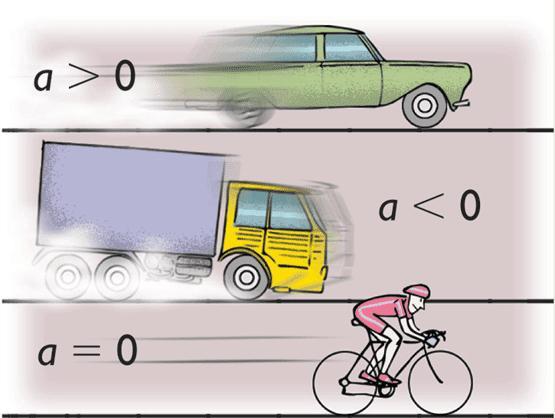
Движение, при котором ускорение тела постоянно, называется равноускоренным. При этом знак ускорения не играет роли. Движение с постоянным отрицательным ускорением также является равноускоренным, несмотря на то, что скорость уменьшается.

Наиболее частым примером равноускоренного движения является свободное падение тел в первые секунды, когда сопротивление воздуха ещё не играет большой роли. Другим примером может служить разгон автомобиля при постоянном нажатии на педаль «газа», пока не будет набрана необходимая скорость.

Формулы равноускоренного движения

Найдём формулы скорости и координаты при равноускоренном движении. Из приведённого выше определения ускорения следует, что скорость при постоянном ускорении равна:

$$\overrightarrow v= \overrightarrow + \overrightarrow a t$$

$$\overrightarrow x= <(\overrightarrow + \overrightarrow v)\over 2> t$$

Что мы узнали?

Ускорение — это физическая величина, характеризующая быстроту набора скорости материальной точкой. Движение с постоянным ускорением называется равноускоренным. Хорошим примером равноускоренного движения является свободное падение тел.

Источник

Равноускоренное движение

Ускорение – физическая величина, показывающая быстроту изменения скорости. Ускорение равно отношению изменения скорости за промежуток времени к величине этого промежутка

Если ускорение и скорость тела направлены в одну сторону, то модуль скорости тела увеличивается, оно разгоняется.

Если ускорение и скорость тела направлены в разные стороны, то модуль скорости тела уменьшается, тело тормозит.

Ускорение в системе СИ измеряется в м/с 2 (метрах, деленных на секунду в квадрате).

Так как ускорение при данном виде движения остается неизменным, то скорость является линейной функцией и вычисляется по формуле:

Перемещение можно рассчитать, применяя следующие формулы:

Обратим внимание, что вторую формулу удобно использовать в задачах, где не дано время движения.

Для прямолинейного равноускоренного движения закон движения выглядит следующим образом:

В записанных уравнениях постановка знаков ± связана со знаками проекций величин скорости, ускорения и перемещения.

Рассмотрим основные графики величин для равноускоренного прямолинейного движения.

Так как модуль ускорения при равноускоренном движении со временем не изменяется, то его график будет представлен в виде прямой линии, параллельной оси времени.

Рис.2.
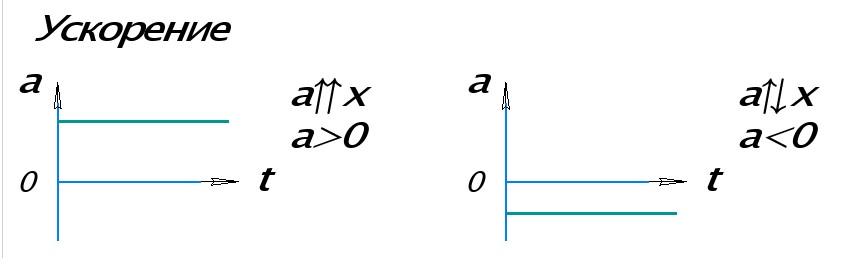
Графики ускорения при равноускоренном прямолинейном движении

На левом рисунке проекция ускорения на ось ОХ, вдоль которой движется тело, положительная. Поэтому график ускорения лежит выше горизонтальной оси t. На правом рисунке ускорение направлено против оси ОХ, его проекция отрицательная. График лежит ниже оси t.

Так как величина скорости тела при данном виде движения рассчитывается по формуле

то ее график будет выглядеть как линейная функция (прямая, расположенная под углом к оси t, исходящая из точки начальной скорости).

На графике слева проекция скорости положительная (υ>0), проекция ускорения тоже положительная (a>0), т.к. скорость тела возрастает со временем. График лежит выше оси t.

На графике справа тело перемещается в направлении, обратном направлению оси ОХ, поэтому проекция скорости отрицательна. Проекция ускорения тоже отрицательна (a 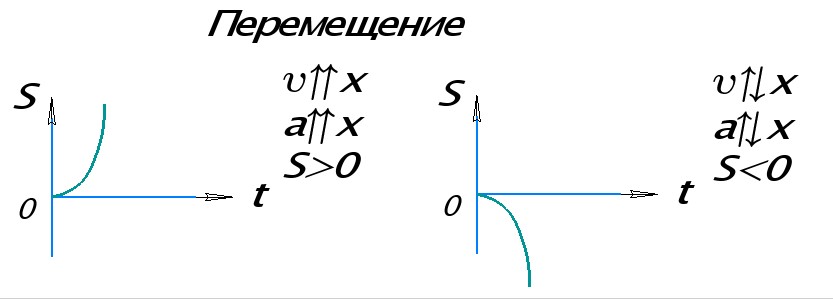Рис.4. Графики перемещения при равноускоренном прямолинейном движении

Если ветвь параболы направлена вверх на графике, значит ускорение на этом участке сонаправлено с осью ОХ. Если ветвь параболы направлена вниз, то ускорение направлено против оси ОХ.

График координаты тела представляет собой график перемещения с учетом начальной координаты x₀.

Остальные тонкости анализа графиков прямолинейного движения будут рассмотрены в отдельной главе.

Источник

Понятие о равноускоренном движении. Формулы перемещения и скорости. Равноускоренное вращение

Движение с ускорением различных объектов окружает нас каждый день. Достаточно лишь вспомнить автомобили, самолеты, велосипеды, вращающиеся колеса и валы, чтобы понять всю важность ускоренного перемещения тел в жизни человека. Для описания этого движения в физике существует специальный раздел, он называется кинематикой. В данной статье рассмотрим, какими формулами описывается перемещение при равноускоренном движении.

Понятие об ускорении, скорости и пути

Вам будет интересно: «Тлетворный» — это о разложении

Прежде чем записывать формулы перемещения при равноускоренном движении, следует дать понятие основным величинам, которые в них фигурируют.

Начнем с пути. Под этой величиной понимают расстояние, которое проходит тело за интервал времени, двигаясь по известной траектории. Чем за более короткое время тело проходит некоторый путь L, тем больше его скорость. Таким образом, скоростью тела является быстрота преодоления им расстояний в пространстве. В данный момент времени расчет скорости выполняют по такой формуле:

Если наблюдать за телом, движущимся вдоль траектории некоторое время, и в каждой точке траектории измерять его скорость, то окажется, что она постоянно меняется. Изменение скорости характеризуют ускорением. В соответствии с определением ускорения оно вычисляется так:

Ускорение также является величиной векторной, только с направлением скорости оно не имеет ничего общего. Вектор ускорения повернут в сторону изменения скорости за данное время или, что одно и то же, в сторону действующей на тело силы.

Равноускоренное движение в физике

Чтобы понять, что такое равноускоренное перемещение, приведем следующий пример: предположим, что автомобиль находился в покое. Затем он начал движение, постоянно увеличивая свою скорость. Если за равные промежутки времени прирост модуля скорости автомобиля был одинаковым, то можно говорить о равноускоренном движении тела. Иными словами, во время рассматриваемого вида перемещения ускорение является величиной постоянной (a = const).

Не стоит думать, что движение с постоянным ускорением может только увеличивать скорость. В результате такого перемещения скорость тела может также уменьшаться до полной его остановки. Такая ситуация возникает, когда транспортное средство осуществляет процесс торможения. В этом случае ускорение будет направлено против вектора скорости.

В природе распространенным движением с постоянным ускорением является падение тел. До определенных скоростей, когда сопротивлением воздуха можно пренебречь, свободное падения является равноускоренным, причем величина ускорения равна 9,81 м/с2.

Изменение скорости при движении с постоянным ускорением

В отличие от ускорения, скорость при равноускоренном движении постоянной величиной не является. Рассмотрим для простоты перемещение по прямой линии. В случае если вектора величин a¯ и v¯ совпадают, имеет место следующая формула для скорости:

Это выражение предполагает, что до появления ускорения тело уже обладало некоторой скоростью v0.

Данная формула показывает, что скорость линейно возрастает с течением времени. График функции v(t) представляет собой прямую линию, которая пересекает ось y на расстоянии v0 от начала координат.

При равноускоренном движении скорость также может уменьшаться линейно. Для этого необходимо, чтобы вектора ускорения и скорости были противоположными (торможение автомобиля, свободный взлет тела в высоту). Для этого случая можно записать такое выражение:

Как и в предыдущем случае, графиком равенства является прямая, только коэффициент ее наклона к оси x будет не положительным, а отрицательным.

Перемещение при равноускоренном движении

Формула пути однозначно получается, если взять интеграл по времени от скорости. В случае когда скорость тела увеличивается, для пути можно записать следующее выражение:

Видно, что графиком функции L(t) является парабола (ее правая ветвь). То есть пройденный путь с течением времени быстро увеличивается.

Если ускорение приводит к уменьшению скорости, тогда формула перемещения при равноускоренном движении примет вид:

Графиком для этого уравнения тоже будет парабола, однако ее ветвь постепенно приближается к некоторому постоянному значению. Последнее соответствует пройденному пути до остановки движущегося тела.

Движение с постоянным ускорением по окружности

Чтобы полнее охарактеризовать тему, следует также привести формулы перемещения при равноускоренном движении по окружности. В отличие от прямолинейного движения, этот вид перемещения описывается угловыми величинами. Тем не менее угловые величины являются полными аналогами соответствующих линейных характеристик.

Для скорости при равноускоренном движении вращения справедлива формула:

Аналогом пути для вращения является угол поворота θ. Для него справедлива формула:

Таким образом, при равноускоренном вращении формулы кинематики сохраняют свой вид, но в них стоят уже угловые физические величины.

Источник