в чем разница между дисперсией и средним квадратическим отклонением
Стандартное отклонение
Стандартное отклонение (англ. Standard Deviation) — простыми словами это мера того, насколько разбросан набор данных.
Вычисляя его, можно узнать, являются ли числа близкими к среднему значению или далеки от него. Если точки данных находятся далеко от среднего значения, то в наборе данных имеется большое отклонение; таким образом, чем больше разброс данных, тем выше стандартное отклонение.
Стандартное отклонение обозначается буквой σ (греческая буква сигма).
Стандартное отклонение также называется:
Использование и интерпретация величины среднеквадратического отклонения
Стандартное отклонение используется:
Рассмотрим два малых предприятия, у нас есть данные о запасе какого-то товара на их складах.
| День 1 | День 2 | День 3 | День 4 | |
|---|---|---|---|---|
| Пред.А | 19 | 21 | 19 | 21 |
| Пред.Б | 15 | 26 | 15 | 24 |
В обеих компаниях среднее количество товара составляет 20 единиц:
Однако, глядя на цифры, можно заметить:
Если рассчитать стандартное отклонение каждой компании, оно покажет, что
Стандартное отклонение показывает эту волатильность данных — то, с каким размахом они меняются; т.е. как сильно этот запас товара на складах компаний колеблется (поднимается и опускается).
Расчет среднеквадратичного (стандартного) отклонения
Формулы вычисления стандартного отклонения
Разница между формулами S и σ («n» и «n–1»)
Состоит в том, что мы анализируем — всю выборку или только её часть:
Как рассчитать стандартное отклонение?
Пример 1 (с σ)
Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.
| День 1 | День 2 | День 3 | День 4 | |
| Пред.Б | 15 | 26 | 15 | 24 |
Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:
Применяем эти шаги:
1. Найти среднее арифметическое выборки:
μ = (15 + 26 + 15+ 24) / 4 = 20
2. От каждого значения выборки отнять среднее арифметическое:
3. Каждую полученную разницу возвести в квадрат:
4. Сделать сумму полученных значений:
5. Поделить на размер выборки (т.е. на n):
6. Найти квадратный корень:
Пример 2 (с S)
Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.
У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.
Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.
| Яблоня 1 | Яблоня 2 | Яблоня 3 | Яблоня 4 | Яблоня 5 | Яблоня 6 |
| 9 | 2 | 5 | 4 | 12 | 7 |
Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:
Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.
Применяем практически те же шаги:
1. Найти среднее арифметическое выборки:
Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5
2. От каждого значения выборки отнять среднее арифметическое:
X1 – Xср = 9 – 6,5 = 2,5
X2 – Xср = 2 – 6,5 = –4,5
X3 – Xср = 5 – 6,5 = –1,5
X4 – Xср = 4 – 6,5 = –2,5
X5 – Xср = 12 – 6,5 = 5,5
X6 – Xср = 7 – 6,5 = 0,5
3. Каждую полученную разницу возвести в квадрат:
4. Сделать сумму полученных значений:
Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5
5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):
(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1
6. Найти квадратный корень:
S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193
Дисперсия и стандартное отклонение
Стандартное отклонение равно квадратному корню из дисперсии (S = √D). То есть, если у вас уже есть стандартное отклонение и нужно рассчитать дисперсию, нужно лишь возвести стандартное отклонение в квадрат (S² = D).
Дисперсия — в статистике это «среднее квадратов отклонений от среднего». Чтобы её вычислить нужно:
Ещё расчёт дисперсии можно сделать по этой формуле:
Правило трёх сигм
Это правило гласит: вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три стандартных отклонения (на три сигмы), почти равна нулю.
Глядя на рисунок нормального распределения случайной величины, можно понять, что в пределах:
Это означает, что за пределами остаются лишь 0,28% — это вероятность того, что случайная величина примет значение, которое отклоняется от среднего более чем на 3 сигмы.
Стандартное отклонение в excel
Вычисление стандартного отклонения с «n – 1» в знаменателе (случай выборки из генеральной совокупности):
1. Занесите все данные в документ Excel.
2. Выберите поле, в котором вы хотите отобразить результат.
3. Введите в этом поле «=СТАНДОТКЛОНА(«
4. Выделите поля, где находятся данные, потом закройте скобки.
5. Нажмите Ввод (Enter).
В случае если данные представляют всю генеральную совокупность (n в знаменателе), то нужно использовать функцию СТАНДОТКЛОНПА.
Коэффициент вариации
Коэффициент вариации — отношение стандартного отклонения к среднему значению, т.е. Cv = (S/μ) × 100% или V = (σ/X̅) × 100%.
Стандартное отклонение делится на среднее и умножается на 100%.
Можно классифицировать вариабельность выборки по коэффициенту вариации:
Какая разница между дисперсией и стандартным отклонением?
Мне было интересно, какова разница между дисперсией и стандартным отклонением.
Если вы рассчитываете два значения, становится ясно, что вы получаете стандартное отклонение от дисперсии, но что это означает с точки зрения распределения, которое вы наблюдаете?
Кроме того, зачем вам стандартное отклонение?
Вам не нужны оба. У каждого из них разные цели. SD обычно более полезен для описания изменчивости данных, в то время как дисперсия обычно намного полезнее математически. Например, сумма некоррелированных распределений (случайных величин) также имеет дисперсию, которая является суммой дисперсий этих распределений. Это не было бы верно для SD. С другой стороны, SD имеет удобство выражаться в единицах исходной переменной.
Если Джон ссылается на независимые случайные величины, когда говорит «несвязанные распределения», то его ответ правильный. Однако, чтобы ответить на ваш вопрос, есть несколько моментов, которые можно добавить:
Среднее значение и дисперсия являются двумя параметрами, которые определяют нормальное распределение.
k ‘ role=»presentation»> k
z ‘ role=»presentation»> z 0 ‘ role=»presentation»> 0 t ‘ role=»presentation»> T
68 % ‘ role=»presentation»> 68 % 1 ‘ role=»presentation»> 1 95.4 % ‘ role=»presentation»> 95.4 % 2 ‘ role=»presentation»> 2 99 % ‘ role=»presentation»> 99 % 3 ‘ role=»presentation»> 3
Погрешность выражается в виде кратного стандартного отклонения оценки.
Дисперсия и смещение являются мерами неопределенности в случайной величине. Среднеквадратичная ошибка для оценки равна дисперсии + квадратное смещение.
Русские Блоги
Стандартизация и нормализация данных
Нормализация характеристик, стандартизованное понимание
Если набор данных стандартизирован, он будет иметь хороший эффект оптимизации для многих алгоритмов машинного обучения (включая градиентный спуск). Если данные не стандартизированы (например, когда функции набора данных различаются на порядок), многие алгоритмы работают плохо.
Сначала поймите разницу между дисперсией, стандартным отклонением и среднеквадратичной ошибкой.
Дисперсия (дисперсия)
Измерьте степень дисперсии (отклонения) случайной величины или набора данных
В теории вероятностей дисперсия используется для измерения степени отклонения между случайной величиной и ее математическим ожиданием (средним).
В статистике сумма квадратов разницы между каждыми данными и их средним значением.
Зачем использовать стандартное отклонение
Согласно вышеизложенному, мы знаем, что дисперсия используется для измерения степени дисперсии (отклонения) случайной величины или набора данных. Формула для стандартного отклонения (также называемая среднеквадратической ошибкой): σ = D ( x ) \sigma = \sqrt
Разница между стандартным отклонением (среднеквадратичной ошибкой) и среднеквадратичной ошибкой
Стандартизация и нормализация данных
Стандартизация данных заключается в пропорциональном масштабировании данных для снятия ограничений между данными и преобразовании их в безразмерные данные для облегчения взвешивания и сравнения различных индексных данных. Нормализацию можно назвать своего рода стандартизацией (стандартизация и нормализация данных). Обычно используемые для непрерывных значений, дискретные значения обычно используют labelencoding и onehot для преобразования данных).
Текущие методы стандартизации данных в основном делятся на следующие три типа:
Линейный метод (пороговый метод: метод экстремальных значений и т. Д., Стандартизация, метод удельного веса)
Ломаная линия
Тип кривой
Различные методы стандартизации по-разному влияют на результаты оценки системы, и вы можете попробовать несколько раз во время обучения машинному обучению.
Цель нормализации
Повышена скорость сходимости модели
Повысьте точность модели
Когда дело доходит до модели расчета расстояния, если значение объекта сильно отличается, оно будет доминировать в процессе расчета, а объект с небольшим значением может привести к недостатку информации (изменение значения почти не влияет на окончательный результат расчета. влияний). Следовательно, чтобы модель могла полностью изучить информацию о каждой функции, мы должны стандартизировать данные во время анализа модели. Численная стандартизация в основном включает гомотактическую обработку данных и обработку размерностей данных.
Кохемотаксис данных в основном решает проблемы различной природы. Поскольку индикаторы разной природы не могут быть напрямую добавлены для обработки, они преобразуются в одно и то же состояние распределения (стандартное нормальное распределение), так что все индикаторы имеют одинаковое влияние на план оценки. Правильный результат можно получить, сложив.
Безразмерные данные в основном предназначены для решения проблемы сопоставимости данных. Своевременные данные находятся в одном и том же состоянии распределения. Если операция нормализации данных не выполняется между различными характеристиками, всегда будут преобладать более крупные характеристики.
Следовательно, нормализация предназначена для того, чтобы функции между различными измерениями имели определенную степень численного сравнения, что может значительно повысить точность классификатора.
Часто используемые методы и характеристики нормализации данных
(1) Мин-макс нормализация
(2) Метод стандартизации Z-баллов (нормализация с нулевым средним)
метод стандартизации и нормализации sklearn
Мы можем использовать связанные классы, предоставленные в sklearn, для стандартизации набора данных, которые могут преобразовывать функции в один и тот же порядок величины, тем самым устраняя влияние различных порядков величины на алгоритм. Два часто используемых метода:
Интеллектуальная рекомендация
Tree Дерево отрезков линии】 COGS 2632
Ссылочный блогАвтор:dreaming__ldxИсточник: CSDN Портал последовательности операций 【Название описания】 Последовательность длины n, вес порядкового номера в начале равен 0, есть m операций Поддерживают.
PAT-A-1046 кратчайшее расстояние [префикс и]
The task is really simple: given N exits on a highway which forms a simple cycle, you are supposed to tell the shortest distance between any pair of exits. Input Specification: Each input fi.
Как нарисовать несколько линий ROC на одном графике?
Класс коллекции JAVA
Резюме JAVA-коллекции Один, коллекция 1. Характеристики коллекций: коллекции используются только для хранения объектов, длина коллекции является переменной, и в коллекции могут храниться объекты разны.
MySQL репликация главный-подчиненный + переключатель главный-подчиненный
MySQL репликация главный-подчиненный + переключатель главный-подчиненный 05 января 2018 10:46:35Протрите протирать прыжок Количество просмотров: 5183Более Персональная категория:база данныхЭксплуатаци.
Стандартное отклонение против дисперсии: в чем разница?
Опубликовано 05.06.2021 · Обновлено 05.06.2021
Стандартное отклонение и дисперсия – это основные математические концепции, которые играют важную роль во всем финансовом секторе, включая области бухгалтерского учета, экономики и инвестирования. В последнем случае, например, твердое понимание расчета и интерпретации этих двух измерений имеет решающее значение для создания эффективной торговой стратегии.
Стандартное отклонение и дисперсия определяются с использованием среднего значения группы рассматриваемых чисел. Среднее значение – это среднее значение группы чисел, а дисперсия измеряет среднюю степень, в которой каждое число отличается от среднего. Степень дисперсии коррелирует с размером общего диапазона чисел – это означает, что дисперсия больше, когда диапазон чисел в группе более широкий, и дисперсия меньше, когда диапазон чисел более узкий.
Ключевые выводы
Стандартное отклонение
Стандартное отклонение – это статистика, которая определяет, насколько далеко от среднего находится группа чисел, с помощью квадратного корня из дисперсии. При вычислении дисперсии используются квадраты, потому что они больше взвешивают выбросы, чем данные, близкие к среднему. Этот расчет также не позволяет разницам выше среднего уравнять те, что ниже, что приведет к нулевой дисперсии.
Стандартное отклонение рассчитывается как квадратный корень из дисперсии путем вычисления отклонения между каждой точкой данных относительно среднего значения. Если точки находятся дальше от среднего значения, в пределах даты имеется большее отклонение; если они ближе к среднему, то отклонение меньше. Таким образом, чем шире группа чисел, тем выше стандартное отклонение.
Дисперсия
Дисперсия – это среднее значение квадратов отличий от среднего. Чтобы вычислить дисперсию, сначала вычислите разницу между каждой точкой и средним значением; затем возведите в квадрат и усредните результаты.
Например, если группа чисел находится в диапазоне от 1 до 10, среднее значение будет 5,5. Если возвести разницу между каждым числом и средним значением, а затем найти их сумму, результат будет 82,5. Чтобы вычислить дисперсию, разделите сумму 82,5 на N-1, который равен размеру выборки (в данном случае 10) минус 1. В результате получится дисперсия 82,5 / 9 = 9,17. Стандартное отклонение – это квадратный корень из дисперсии, поэтому стандартное отклонение составляет около 3,03.
Из-за этого возведения в квадрат дисперсия больше не находится в той же единице измерения, что и исходные данные. Выявление корня из дисперсии означает, что стандартное отклонение восстанавливается до исходной единицы измерения и, следовательно, его гораздо легче интерпретировать.
Стандартное отклонение и дисперсия при инвестировании
Для трейдеров и аналитиков эти две концепции имеют первостепенное значение, поскольку они используются для измерения безопасности и волатильности рынка, что, в свою очередь, играет большую роль в создании прибыльной торговой стратегии.
Стандартное отклонение – один из ключевых методов, используемых аналитиками, управляющими портфелями и консультантами для определения риска. Когда группа чисел ближе к среднему, вложение менее рискованно; когда группа чисел дальше от среднего, инвестиции представляют больший риск для потенциального покупателя.
Ценные бумаги, которые близки к своим средствам, считаются менее рискованными, поскольку они с большей вероятностью будут продолжать вести себя как таковые. Ценные бумаги с большими торговыми диапазонами, которые имеют тенденцию к резкому скачку или изменению направления, более рискованны. При инвестировании риск сам по себе не является плохой вещью, поскольку чем рискованнее безопасность, тем больше вероятность выплаты.
Стандартное отклонение и дисперсия – два разных математических понятия, которые тесно связаны. Дисперсия необходима для расчета стандартного отклонения. Эти числа помогают трейдерам и инвесторам определять волатильность инвестиций и, следовательно, позволяют им принимать обоснованные торговые решения.
Среднее отклонение, стандартное отклонение и дисперсия в обработке сигналов
В данной статье рассматриваются три описательных статистических меры с точки зрения приложений обработки сигналов.
В предыдущей статье, посвященной описательной статистике для инженеров-электронщиков, мы увидели, что центральную тенденцию набора данных могут передавать как среднее арифметическое, так и медиана. Несмотря на то, что медиана менее чувствительна к выбросам, в электронике и цифровой обработке сигналов чаще используется среднее арифметическое. Среднее арифметическое, по сути, является основным статистическим методом в электротехнике.
Однако для адекватного описания или понимания набора данных нам часто требуется нечто большее, чем только среднее арифметическое.
Когда мы сообщаем только о центральной тенденции, мы не учитываем важный аспект данных, а именно то, каким образом значения отклоняются от центральной тенденции.
Отклонение от среднего значения
Давайте представим, что мы оцифровали два аналоговых входных сигнала. Если мы преобразуем цифровые коды обратно в единицы вольт и построим графики по времени, они будут выглядеть следующим образом:
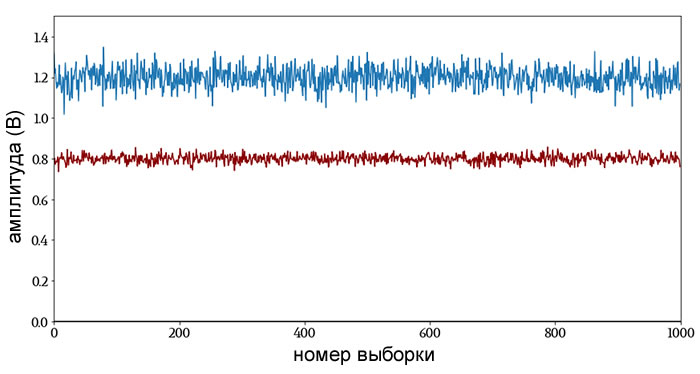
Мы можем довольно хорошо угадать средние значения, просто взглянув на график: центральная тенденция синего сигнала равна 1,2 В, а красного сигнала – 0,8 В. Но если мы сообщим только о средних значениях, мы создадим впечатление, что единственное важное различие между этими двумя сигналами – это разница средних значений 0,4 В (или мы можем назвать это уровнем постоянной составляющей или смещением по постоянному напряжению). Очевидно, что это еще не всё.
Инженер-электронщик интуитивно идентифицирует эти сигналы как устойчивые сигналы постоянного напряжения (возможно, напряжения питания), которые содержат довольно много шума.
Что еще более важно, мы немедленно признаем, что синий сигнал значительно более шумный, чем красный сигнал. Это основное различие в шумовых характеристиках теряется, если рассматривать только среднее значение.
Кстати, почему мы замечаем шум в этих сигналах? Так как
Когда статистик видит небольшие случайные отклонения от среднего значения, инженер-электронщик видит шум.
Среднее отклонение
Насколько шумные эти сигналы? Довольно шумные? Очень шумные? Попробуем дать более точный ответ на этот вопрос. Другими словами, нам нужно количественно определить отклонение в этих наборах данных.
Моя первая мысль при измерении отклонения состоит в том, чтобы найти расстояние между каждой точкой данных и средним значением, а затем вычислить среднее значение всех этих расстояний. Это даст нам среднее отклонение (также называемое средним абсолютным отклонением, MAD, mean absolute deviation), то есть типовое значение, на которое значения отклоняются от центральной тенденции. Ниже показана формула среднего отклонения:
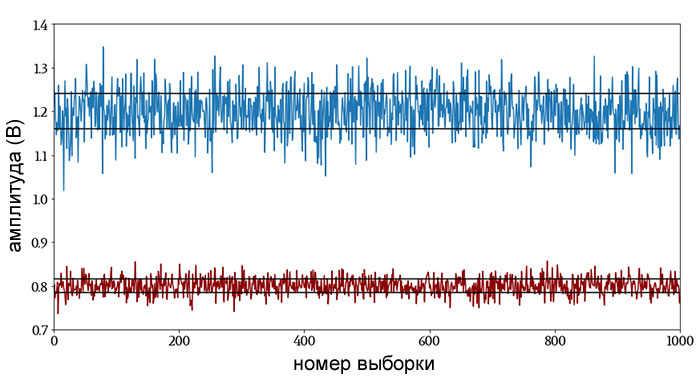
Хотя среднее отклонение интуитивно понятно, оно не является самым распространенным методом количественной оценки склонности сигнала отклоняться от среднего значения. Для этого нам нужно стандартное отклонение.
Дисперсия и стандартное отклонение
В области электротехники проблема со средним отклонением состоит в том, что мы усредняем разности напряжений (или токов), и, следовательно, работаем в области амплитуд. Природа шумовых явлений такова, что при анализе шума мы делаем упор на мощности, а не на амплитуды, и, следовательно, нам нужен статистический метод, который работает в области мощностей.
К счастью, это просто. Мощность пропорциональна квадрату напряжения или тока, и, следовательно, всё, что нам нужно сделать, это возвести разность в квадрат до суммирования и усреднения. Результатом этой процедуры является статистическая мера, называемая дисперсией, обозначаемая σ 2 (сигма в квадрате):
Мы можем описать дисперсию как усредненную мощность случайных отклонений сигнала, выраженную в виде мощности. Это означает, что единица измерения дисперсии будет отличаться единицы измерения значений, с которых мы начинали. Если мы анализируем колебания в сигнале напряжения, дисперсия имеет единицы измерения В 2 вместо В.
Если мы хотим выразить склонность сигнала отклоняться случайным образом, используя исходную единицу измерения, мы должны компенсировать возведение в квадрат каждой разности, применив к конечному значению квадратный корень:
Эта процедура генерирует статистическую меру, известную как стандартное отклонение, то есть усредненную мощность случайных отклонений сигнала, выраженную в виде амплитуды. Таким образом, если мы анализируем сигнал напряжения, стандартное отклонение имеет единицы измерения В, несмотря на то, что мы вычислили стандартное отклонение, используя квадрат отклонений напряжения.
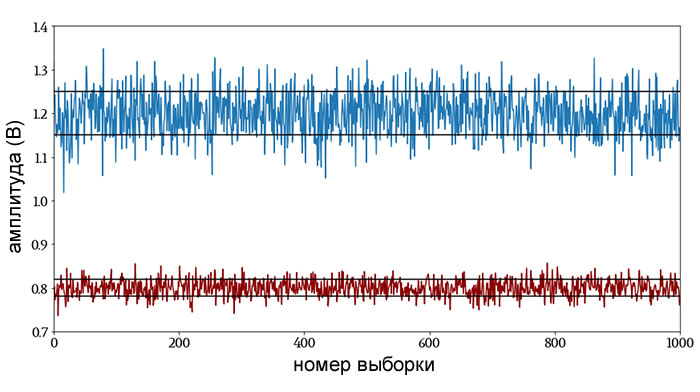
Дисперсия и стандартное отклонение по-разному выражают одну и ту же информацию. Хотя дисперсия, насколько я понимаю, более удобна в определенных аналитических ситуациях, стандартное отклонение обычно предпочтительнее, поскольку это число, которое можно непосредственно интерпретировать, как меру склонности сигнала отклоняться от среднего значения.
Заключение
Стандартное отклонение и дисперсия являются важными статистическими методами, которые часто фигурируют в технических и общественных науках. Я надеюсь, что данная статья помогла вам понять основную связь между этими понятиями и электрическими сигналами, и в следующей статье мы рассмотрим некоторые интересные подробности, связанные со стандартным отклонением.












