время релаксации в чем измеряется
Время релаксации
Время релаксации — период времени, за который амплитудное значение возмущения в выведенной из равновесия физической системе уменьшается в e раз (e — основание натурального логарифма), в основном обозначается греческой буквой τ.
Согласно принципу Ле Шателье — Брауна при отклонении физической системы от состояния устойчивого равновесия возникают силы, которые пытаются вернуть систему к равновесному состоянию. Если в состоянии равновесия некоторая физическая величина f имеет значение 


где λ — некоторый параметр, а знак минус указывает на то, что реакция системы на возмущение приводит к возвращению к равновесному состоянию.
В таком случае величина f будет изменяться по закону:

где 
Использование
Приближение времени релаксации широко используется при описании кинетических процессов в физике, когда речь идет о кинетике установления равновесного состояния. Переход от неравновесного состояния к равновесию сопровождается диссипацией энергии и является необратимым процессом. Установление равновесия часто проходит в несколько этапов, которые характеризуются своими отдельными временами релаксации. Так, при возбуждении молекул светом установление теплового равновесия происходит за время порядка 
При описании многих физических процессов время релаксации берётся как феноменологический параметр, однако в отдельных случаях его можно определить через параметры микроскопических процессов, таких как вероятность квантовомеханического перехода или сечение рассеяния.
См. также
Полезное
Смотреть что такое «Время релаксации» в других словарях:
время релаксации — электрической поляризации; время релаксации Время, в течение которого поляризованность диэлектрика после снятия внешнего электрического поля уменьшается в e раз, где e основание натуральных логарифмов. Время, в течение которого отклонение системы … Политехнический терминологический толковый словарь
время релаксации — Время, в течение которого напряжения при релаксации уменьшаются в е раз (е = 2,718. ). [Сборник рекомендуемых терминов. Выпуск 82. Строительная механика. Академия наук СССР. Комитет научно технической терминологии. 1970 г.] Тематики… … Справочник технического переводчика
Время релаксации — – время, в течение которого напряжения при релаксации уменьшаются в е раз (е = 2,718….). [Строительная механика. Терминология. Выпуск 82. Изд. «Наука» М.1970] Рубрика термина: Теория и расчет конструкций Рубрики энциклопедии:… … Энциклопедия терминов, определений и пояснений строительных материалов
время релаксации — relaksacijos trukmė statusas T sritis chemija apibrėžtis Laikas, per kurį kurio nors dydžio nuokrypis nuo pusiausvirojo sumažėja e kartų. atitikmenys: angl. relaxation time rus. время релаксации; период релаксации … Chemijos terminų aiškinamasis žodynas
время релаксации — relaksacijos trukmė statusas T sritis fizika atitikmenys: angl. relaxation time vok. Erholungszeit, f; Relaxationszeit, f rus. время релаксации, n; период релаксации, m pranc. temps de relaxation, m … Fizikos terminų žodynas
ВРЕМЯ РЕЛАКСАЦИИ — – характерное время приближения системы к равновесному состоянию. В магнетизме – характеристика способности магнитных зерен или доменов в них менять направление намагниченности. Мелкие зерна магнитных минералов, время релаксации магнитных… … Палеомагнитология, петромагнитология и геология. Словарь-справочник.
время релаксации — relaksacijos trukmė statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, atvirkščiai proporcingas sistemos slopimo koeficientui, t. y. τ = 1/δ ; čia δ – slopimo koeficientas. atitikmenys: angl. relaxation time vok. Relaxationszeit,… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
время релаксации — relaksacijos trukmė statusas T sritis Standartizacija ir metrologija apibrėžtis Eksponentinio grįžimo į pusiausvyrą vyksmo trukmės konstanta. atitikmenys: angl. relaxation time vok. Relaxationszeit, f rus. время релаксации, n pranc. constante de… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
время релаксации — relaksacijos trukmė statusas T sritis Standartizacija ir metrologija apibrėžtis Laiko tarpas, per kurį tam tikro dydžio vertės nuokrypis nuo pradinės arba pusiausvirosios vertės sumažėja e (e = 2,71828…) kartų. atitikmenys: angl. relaxation time… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
ВРЕМЯ РЕЛАКСАЦИИ
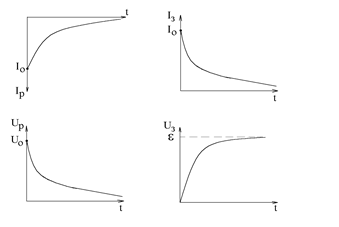
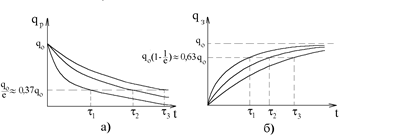
Зависимости силы тока и разности потенциалов при зарядке и разрядке конденсатора носит экспоненциальную зависимость, которая определяется величиной параметра tтеор= RC (рис.3).
Это произведение имеет размерность времени. Из дифференциальных уравнений видно, что время релаксации t есть величина обратная скорости изменения заряда на обкладках конденсатора.
Отсюда следует, что чем больше t, тем медленнее будет уменьшаться с течением времени множитель 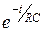
Таким образом, постоянная времени t характеризует длительность переходных процессов, происходящих в цепи. За время t=t заряд конденсатора либо уменьшается в e раз при разрядке конденсатора, либо достигает значения в e раз меньшего, чем максимальное q0 при его зарядке.
Имея экспоненциальные кривые напряжения или тока, можно найти постоянную времени цепи tэксп. Для этого на графике U(t) или I(t) при разрядке и зарядке выбирают уровень 
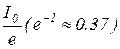

Исследование переходных процессов при зарядке и разрядке конденсаторов, построение экспоненциальных кривых, определение постоянной времени и является целью данной лабораторной работы.
Для проверки экспоненциальной зависимости и определения времени релаксации используют другой метод. Если прологарифмировать (8) и (12), то получим зависимости типа:
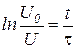
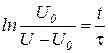
Построив графики зависимости 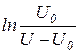
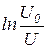

Время релаксации и длина свободного пробега



Выясним теперь физический смысл коэффициента t.
Предположим, что, после того как скорость направленного движения электронов достигла стационарного значения vД, поле Е выключено. Вследствие столкновений электронов с дефектами решетки эта скорость начнет уменьшаться, и электронный газ будет переходить в равновесное состояние. Такие процессы установления равновесия в системе, ранее выведенной из этого состояния, называют релаксацией. Полагая в (5.3) qЕ=0, получим уравнение, описывающее переход электронного газа в равновесное состояние — процесс его релаксации:
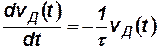
Интегрируя (5.6), находим
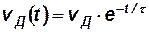
Движение электронов в кристалле удобно описывать, используя понятие длины свободного пробега. По аналогии с кинетической теорией газов можно считать, что электрон движется в кристалле прямолинейно до тех пор, пока не встретится с дефектом решетки и не рассеется. Средний отрезок пути λ, который проходит электрон между двумя последовательными актами рассеяния, принимается за длину свободного пробега электрона.
Если бы электрон уже в единичном акте рассеяния полностью терял скорость в данном направлении и возвращался в первоначальное состояние хаотического движения, то средняя длина свободного пробега равнялась бы просто произведению средней скорости движения электронов v на время релаксации τ, которое в этом случае представляло бы собой просто время свободного движения электрона:
Часто, однако, для полного уничтожения скорости в данном направлении требуется не одно, а в среднем υ столкновений с рассеивающими центрами. Только после υ столкновений исчезает всякая корреляция между начальной и конечной скоростями движения электронов. Время, в течение которого будет происходить рассасывание направленного движения электронов, и в этом случае представляет собой время релаксации. Но средний путь, который пройдет электрон за это время, равен уже не λ, а
Величину L называют средней транспортной длиной свободного пробега.
Тот факт, что под действием электрического поля Е в проводнике возникает дрейф свободных носителей заряда, приводящий к появлению электрического тока, свидетельствует о том, что поле Е изменяет характер распределения свободных электронов по состояниям, т. е. вид функции распределения f(E), так как равновесная функция распределения f0(Е) не может привести к появлению тока. На рис. 5.1, а, б пунктиром показаны графики функций распределения для электронов после установления постоянной скорости дрейфа. Из рис. 5.1 видно, что влияние внешнего поля E на функцию распределения электронов по состояниям сводится к смещению всего распределения на величину vД=qEτ/mn в направлении, противоположном E. Вследствие такого смещения функции распределения перестают быть симметричными относительно оси ординат, и средняя скорость движения электронов в направлении оси х уже не будет равна нулю, как в отсутствие поля Е. Легко показать, что средняя скорость в этом случае будет равна скорости дрейфа vД.
Релаксация (физика)
СОДЕРЖАНИЕ
В простых линейных системах [ править ]
Механика: демпфированный ненагруженный осциллятор [ править ]
модель глушила невынужденные колебания груза на пружине.
Электроника: RC схема [ править ]
В RC-цепи, содержащей заряженный конденсатор и резистор, напряжение спадает экспоненциально:
В физике конденсированного состояния [ править ]
В физике конденсированного состояния релаксация обычно изучается как линейный отклик на небольшое внешнее возмущение. Поскольку лежащие в основе микроскопические процессы активны даже в отсутствие внешних возмущений, можно также изучать «релаксацию в равновесии» вместо обычной «релаксации в равновесие» (см. Теорему о флуктуационно-диссипации ).
Снятие стресса [ править ]
Время диэлектрической релаксации [ править ]
Жидкости и аморфные твердые тела [ править ]
Термин «структурная релаксация» был введен в научную литературу в 1947/48 г. без какого-либо объяснения применительно к ЯМР и означал то же, что и «тепловая релаксация». [1]
Спиновая релаксация в ЯМР [ править ]
Методы химической релаксации [ править ]
Мономолекулярная обратимая реакция первого порядка [ править ]
Мономолекулярная обратимая реакция первого порядка, близкая к равновесной, может быть представлена следующей символической структурой:
Другими словами, реагент A и продукт B переходят друг в друга на основании констант скорости реакции k и k ‘.
Подставляя это значение вместо [B] через A (0) и A (t), получаем
В атмосферных науках [ править ]
Обесцвечивание облаков [ править ]
В водяных облаках, где концентрации выше (сотни на см 3 ) и температуры выше (что позволяет значительно снизить скорость перенасыщения по сравнению с ледяными облаками), время релаксации будет очень низким (от секунд до минут). [3]
В ледяных облаках концентрации ниже (всего несколько единиц на литр), а температуры ниже (очень высокие скорости перенасыщения), поэтому время релаксации может достигать нескольких часов. Время релаксации представлено как
В астрономии [ править ]
T r = 0.34 σ 3 G 2 m ρ ln Λ <\displaystyle T_
Релаксация (физика)
Механика: Демпфированный ненагруженный осциллятор.
модель глушила невынужденные колебания груза на пружине.
Электроника: RC-схема
В RC-цепи, содержащей заряженный конденсатор и резистор, напряжение спадает экспоненциально:
В физике конденсированного состояния релаксация обычно изучается как линейный отклик на небольшое внешнее возмущение. Поскольку лежащие в основе микроскопические процессы активны даже в отсутствие внешних возмущений, можно также изучать «релаксацию в равновесии» вместо обычной «релаксации в равновесие» (см. Теорему о флуктуационно-диссипации ).
Снятие стресса
Время диэлектрической релаксации
Жидкости и аморфные твердые тела
Термин «структурная релаксация» был введен в научную литературу в 1947/48 г. без какого-либо объяснения применительно к ЯМР и означал то же, что и «тепловая релаксация». [1]
Спиновая релаксация в ЯМР
Мономолекулярная обратимая реакция первого порядка
Мономолекулярная обратимая реакция первого порядка, близкая к равновесной, может быть представлена следующей символической структурой:
Другими словами, реагент A и продукт B переходят друг в друга на основании констант скорости реакции k и k ‘.
Подставляя это значение вместо [B] через A (0) и A (t), получаем
Обесцвечивание облаков
В водяных облаках, где концентрации выше (сотни на см 3 ) и температуры выше (что позволяет значительно снизить скорость перенасыщения по сравнению с ледяными облаками), время релаксации будет очень низким (от секунд до минут). [3]
В ледяных облаках концентрации ниже (всего несколько единиц на литр), а температуры ниже (очень высокие скорости перенасыщения), поэтому время релаксации может достигать нескольких часов. Время релаксации представлено как